2.4.1. Exercices¶
2.4.1.1. Libre parcours moyen¶
L’anémométrie à fil chaud est un procédé permettant de faire des mesures dans un écoulement grâce à un fil de quelques micromètres (typiquement 5 :math:` mu`m). On demande de calculer le nombre de Knudsen pour différents gaz afin de vérifier la qualité des mesures que l’on peut faire sur ces écoulements, ceci dans des conditions standards de température et pression. La théorie cinétique des gaz montre que le libre parcours moyen des gaz obéit à la relation \(\lambda=\frac{\sqrt2\ m}{2 \pi \rho d^2}\) .
\(\rho\) est la densité, m la masse moléculaire et d le diamètre moléculaire approché par des modèles physiques.
| Gaz |
|
Masse moléculaire (* \(*10^{27}\) kg) |
|---|---|---|
| Helium (He) | 2.33 | 6.65 |
| Hydrogène (H) | 2.92 | 3.34 |
| Azote (N) | 4.17 | 46.5 |
| Oxygène (O) | 4.07 | 53.12 |
| Gaz carbonique (CO2) | 5.62 | 73.1 |
- A partir de recherche dans la littérature, trouver les principes de fonctionnement de ce type de sonde.
- Pour chaque composé chimique, évaluer ou trouver comment évaluer d le diamètre moléculaire, calculer d’abord la masse volumique \(\rho\) (aux conditions standards), puis le libre parcours moyen \(\lambda\). En déduire le nombre de Knudsen. Que compare ce nombre sans dimension et quelle conclusion peut-on en tirer?
- Quelle conclusion peut-on en tirer pour l’utilisation d’une sonde à fil chaud.
(Difficulté 2.5/5) Réponse :
| Helium (He) | Hydrogène (H) | Azote (N) | Oxygène (O) | Gaz carbonique (CO2) | |
| \(\lambda\) (nm) | 154 | 197 | 96 | 101 | 26 |
2.4.1.2. Loi d’état et son utilisation¶
Calculer la masse m d’un volume V=3 litres d’huile d’olive ayant une densité d=0,918.
- (Difficulté 1/5) Réponse :
- m=2.754kg
Soit une bouteille qui contient une masse de 1kg de gaz à 25°c (on suppose que ce gaz obéit à la loi des gaz parfaits) Une autre bouteille contient la même masse de gaz, mais un volume 2 fois plus grand. Montrer que la pression dans la seconde bouteille est 2 fois plus petite que celle de la 1ère et ce, quel que soit le gaz.
(Difficulté 1/5)
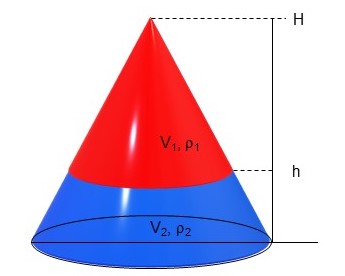
Soit un réservoir de forme conique (la base est de rayon R, la hauteur est H=0.6m) est rempli dans sa partie basse par de l’eau et au-dessus un fluide de masse volumique \(\rho_1 \). Calculer la hauteur h correspondant à l’interface entre l’eau et l’huile de telle façon que la masse des 2 fluides soient identiques.
(Difficulté 3/5) Réponse : h=12 cm
2.4.1.3. Viscosité¶
Déterminer la viscosité dynamique de l’huile d’olive \(\mu_{oil}\) sachant que sa densité est 0,918 et sa viscosité cinématique est 1,089 Stockes.
(Difficulté 1/5) Réponse : \(\mu_{oil} \simeq 0.1\) Pas.
Du fuel porté à une température T=20°C a une viscosité dynamique \(\mu_{fuel}\) Pa.s . Calculer sa viscosité cinématique \(\eta_{fuel}\) en Stockes sachant que sa densité est d=0,95.
(Difficulté 1/5) Réponse : \(\eta_{fuel}\) = 1 St
Expliquer le principe de mesure d’un viscosimètre à chute de bille.
(Difficulté 3/5)
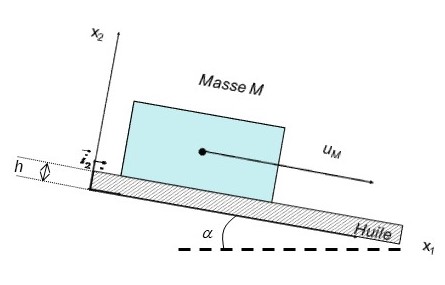
Un objet de masse m=15kg, glisse sur un plan incliné de 10° par rapport à l’horizontale. De l’huile est constamment présente sur ce plan incliné ou du moins sous l’objet pour assurer son déplacement. L’aire A de sa surface en contact avec le fluide est A=1m \(2\). On suppose que l’huile est un fluide newtonien de viscosité dynamique constante \(\mu =10^{-3} Pa.s\). L’épaisseur de la couche de fluide est h=2mm.
- Décrire ce qu’il se passe dans la couche de fluide sous l’objet M.
- Faire le bilan des forces agissant sur l’objet M.
- En déduire une estimation de la vitesse à laquelle l’objet glisse (on suppose qu’un régime stationnaire est atteint).
- (Difficulté 4/5) Réponse
- U=0.5 m/s
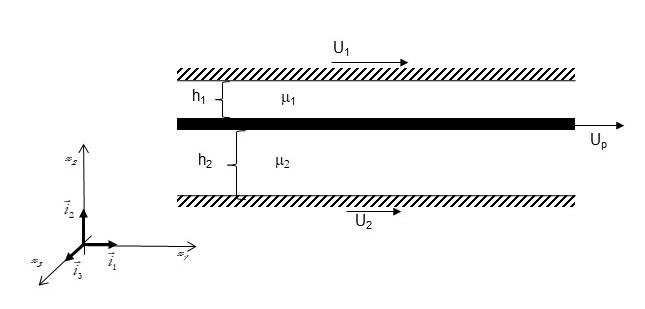
On considère 2 plaques très minces dans un écoulement au-dessus d’une paroi fixe. La plaque 1 est mise en mouvement, on cherche à déterminer la vitesse de la plaque \(U_2\) sachant que \(U_1 = 1.2m/s\).
2 fluides différents s’écoulement entre ces plaques, de viscosité dynamique \(\mu_1 \)mu_2`, telle que \(\frac{\mu_1}{\mu_2}=2.5\) et \(\frac{h_1}{h_2}=\sqrt 2\). On suppose que les hauteurs \(h_1\) et \(h_2\) sont assez faibles et sont dans la couche limite des écoulements.
Calculer la contrainte qu’exerce le fluide 1 sur la plaque 1 sachant que le fluide 1 est de l’eau (on prendra \(\mu_1 =1.10^{-3}\ Pa\ s\)) et en déduire la vitesse de la plaque U2.
(Difficulté 4.5/5) Réponse : \(U_2=3.32 m/s\)
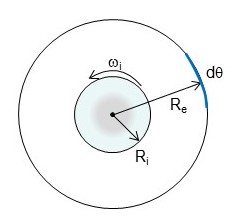
On considère un viscosimètre de Couette constitué de 2 cylindres coaxiaux de hauteur h=0.1m qui contient un fluide de viscosité dynamique \(\mu =0.08 Pa.s\). Le cylindre intérieur de rayon \(R_i = 40 mm\) tourne avec une vitesse \(\omega_i =200 tr/mn\). Le cylindre extérieur de rayon \(R_e = 43 mm\) est maintenu immobile. Calculer la force élémentaire exercée par le fluide sur un élément de surface du cylindre extérieur. En déduire la contrainte totale exercée par le fluide sur ce cylindre et donc le couple à appliquer pour faire tourner le cylindre intérieur. On supposera une forme linéaire de la vitesse entre les 2 plaques.
(Difficulté 5/5) Réponse : \(C =2.25\ 10^{-2}\ N.m\)