3.1. Description du mouvement¶
La difficulté principale de la description du mouvement des fluides est due à la déformation de la particule fluide au cours de son mouvement.
On peut utiliser des représentations habituelles, que sont les représentations lagrangiennes, qui s’inspirent de la Mécanique rationnelle. On pourra reconstruire l’écoulement par le suivi des particules fluides formant cet écoulement.
On peut utiliser une approche eulérienne qui consiste à considérer l’écoulement dans sa globalité (en tout point du domaine \(\mathcal{D}\), pour toutes les grandeurs) et à un instant \(\tau\) donné. C’est comme si l’on photographiait cet écoulement à l’instant \(\tau\), et on ordonne les photos dans l’ordre chronologique pour reconstruire l’écoulement. Les deux méthodes sont fondamentalement différentes mais, comme on va le voir, on peut évidemment passer de l’une à l’autre.
Si on s’intéresse à l’histoire des particules fluides, on utilise la première représentation : par exemple, en faisant un calcul d’aérodynamique autour d’un obstacle, on veut connaître la trajectoire d’une particule fluide (en suivant un marqueur dans un écoulement). Une description eulérienne est beaucoup plus efficace, si on veut calculer l’écoulement autour d’une sonde (thermocouple, mesure de pression), positionnée à un endroit fixe : par sa commodité, cette approche est préférée en Mécanique des Fluides, même si la formulation des principes physiques est plus facile en lagrangien.
important
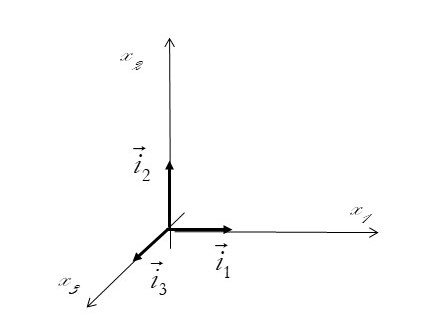
Dans tout ce qui suit, on aura au préalable défini un référentiel « fixe » (celui du laboratoire) muni d’un repère orthonormé \(\mathcal{R}\), avec une base de vecteurs \(\vec{i}_\alpha,\ \alpha=1..3\), les coordonnées sur les axes du repère sont nommées \(x_\alpha,\ \alpha=1..3\).
Figure 3.1 : Base, axes et système de coordonnées dans le repère \(\mathcal{R}\) utilisé dans ce cours.
3.1.1. Description lagrangienne : Particules fluide et Volume matériel¶
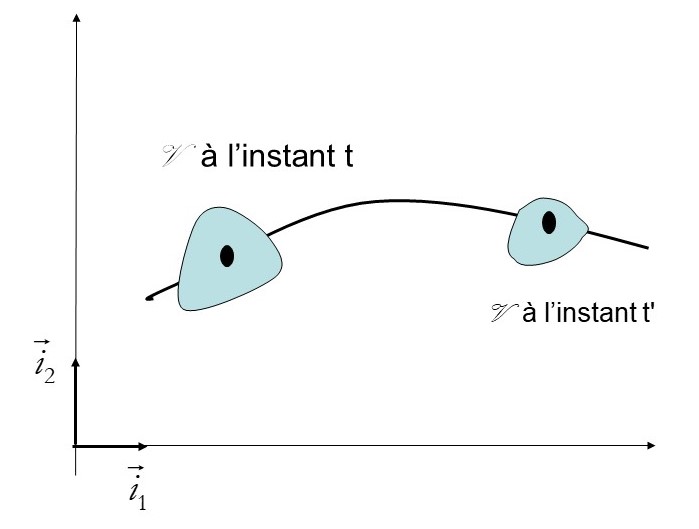
Dans cette approche, on considère une particule fluide \(\mathcal{P_f}\) ou un volume \(\mathcal{V}\) qui contient des particules fluides, que l’on suit au cours du temps. Ce volume est appelé volume matériel :
- Il contient toujours les mêmes particules.
- Au cours du temps, ce volume peut changer de forme et de position.
- On peut lui appliquer des lois de conservation.
On appelle trajectoire les positions successives, que l’on repère par ses coordonnées, \(X(X_1,X_2,X_3)\) de la particule fluide \(\mathcal{P_f}\).
L’expression « suivre \(\mathcal{P_f}\) au cours du temps », signifie que l’on connait alors ses positions dans le domaine \(\mathcal{D}\) de l’écoulement mais aussi son état thermodynamique en chaque instant (masse volumique, pression, température, etc.). C’est comme si un observateur était placé sur cette particule fluide.
Figure 3.2 : Une particule fluide (ou volume) suivie sur sa trajectoire.
3.1.2. Description eulerienne : Volume de contrôle¶
Etudier un écoulement par une approche eulérienne consiste à trouver les caractéristiques des particules fluides qui sont dans un volume de contrôle \(\mathcal{V}\). Ce volume est choisi arbitrairement. Il doit respecter des propriétés :
- Le volume V est défini par son contour \(\mathcal{C}\), et en chaque point de ce contour une normale sortante \(\vec n\).
- Le voisinage du volume ne peut contenir que des particules fluides.
- Dans ce cours on se limitera au cas où le volume reste inchangé au cours du temps, en forme et en position.
Figure 3.3 : Des volumes de contrôle ? Seul celui de droite n’est pas un volume de contrôle .
3.1.3. Variable de Lagrange - Variable d’Euler – Vitesse¶
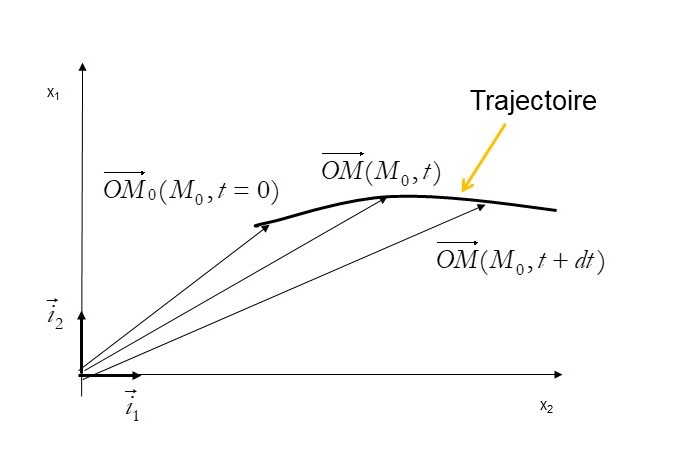
A t=0s, la particule fluide \(\mathcal{P_f}\) est à la position \(M_0=M_0(X_{1,0},X_{2,0},X_{3,0})\), qui définit le vecteur \(\vec{OM_0}\).
Les paramètres \((X_{1,0},X_{2,0},X_{3,0},t)\) sont les coordonnées indépendantes, appelées variables de Lagrange. Ce sont les projections dans un repère de la position sur la trajectoire.
Avertissement
(Attention X n’est pas x!). L’indice « 0 » signifie que l’on est à l’instant 0.
La courbe qui décrit les positions successives de \(\mathcal{P_f}\) s’appelle trajectoire. A un instant t >0s , le volume matériel se trouve en un point M(t) dont les coordonnées ne dépendent que de \(M_0\), qui est une constante, et du temps.
On peut définir alors, le vecteur position à l’instant t, \(\vec{OM}=\vec{OM}(X_{1,0},X_{2,0},X_{3,0},t)\) . Sur la trajectoire, la position ne dépend alors que de la position initiale (très importante!) et du temps.
Figure 3.4 : Représentation d’une trajectoire d’un volume matériel
Le mouvement du fluide est connu si on connait les relations \(\vec{OM}=x_1{\vec{i}}_1+x_2{\vec{i}}_2+x_3{\vec{i}}_3\), soit :
Les \(x_i\) étant les projections sur les axes de référence.
Toute grandeur \(\phi\) associée au volume matériel, donc sur sa trajectoire, dépend du temps et de la position initiale. On a alors: \(\phi = \phi (\vec{OM_0},t)\).
A l’instant t+dt, la position du volume matériel est en \(\mathcal M \prime\) , alors la vitesse, comme en mécanique rationnelle, se calcule par \(\vec{u} = \lim_{dt \to 0} = \frac{ \vec{OM}- \vec{OM'} }{dt}\)
On a donc \(\vec{u} = \frac{d \vec{OM}}{dt}\)
La projection du vecteur \(\vec{OM}\) dans le repère \(\mathcal R\) , \(\vec{OM}=(x_1,x_2,x_3)\) , est donc :
Une représentation eulérienne consiste à décrire l’écoulement dans sa globalité : à un instant donné, on connait pour chaque position \((x_1,x_2,x_3)\) du volume de contrôle (et non plus sur la trajectoire d’une particule fluide), la vitesse, pression, température.
Ainsi une grandeur \(\phi\), dans une approche eulérienne s’écrit : \(\phi=(x_1,{\ x}_2,\ x_3,t)\)
Les variables d’Euler sont donc: \((x_1,{\ x}_2,\ x_3,t)\).
Le champ de vitesse s’écrit alors:
\(\vec{u} = \left \{ \begin{matrix} u_1(x_1,{\ x}_2,\ x_3,t) \\ u_2(x_1,{\ x}_2,\ x_3,t) \\ u_3(x_1,{\ x}_2,\ x_3,t) \\ \end{matrix} \right .\) .
Toute grandeur \(f\) scalaire ou vectorielle de l’écoulement s’écrira \(f ( x_1, {\ x}_2, \ x_3, t)\)
Exemple
Dans le repère \(\mathcal{R}\), un système matériel a son mouvement décrit par \(\left \{ \begin{matrix} x_1 = X_{1,0} f(t) \\ x_2 = X_{2,0} \\ x_3=X_{3,0} \\ \end{matrix} \right .\)
La fonction \(f(t)\) est telle que \(f(0)=0\)
Le vecteur vitesse s’écrit par définition \(\vec{u} = \left \{ \begin{matrix} \frac{{\rm dx}_1}{dt} = X_{1,0} f'(t) \\ \frac{{\rm dx}_2}{dt} = 0 \\ \frac{{\rm dx}_3}{dt} = 0 \\ \end{matrix} \right .\).
Le vecteur position s’écrit donc de manière générale : \(\vec{OM} = \vec{OM} \left( x_1, x_2, x_3 \right)\).
Le vecteur vitesse \(\vec{u}=\frac{\partial \vec{OM}}{\partial t} = \left \{ \begin{matrix} X_{1,0} f'(t)\\ 0 \\ 0 \\ \end{matrix} \right.\) soir en variabless d’Euler : \(\vec{u} = \frac{\partial\vec{OM}}{\partial t}=\left \{ \begin{matrix} x_1\frac{f'(t)}{f(t)} \\ 0 \\ 0\\ \end{matrix} \right.\)
Avertissement
La représentation d’une grandeur physique ne peut pas être la même en Euler ou Lagrange. Mais on confondra les deux écritures. Dans le suivi, on peut associer la température à une particule fluide, tandis que l’on parlera du champ de température de l’écoulement décrit par une approche eulérienne.
3.1.4. Relation entre méthodes Eulérienne et Lagrangienne¶
Soit l’expression du champ de vitesse (méthode Eulérienne) suivant :
(3.3)¶\[\begin{split}\vec{u}=\frac{d\vec{OM}}{dt}=\left\{\begin{matrix}\frac{{dx}_1}{dt}=u_1\left(x_1,x_2,x_3,\ t\right)\\\frac{{dx}_2}{dt}=u_2\left(x_1,x_2,x_3,\ t\right)\\\frac{{dx}_3}{dt}=u_3\left(x_1,x_2,x_3,\ t\right)\\\end{matrix}\right.\end{split}\]
L’intégration du système (Eq. 3.3) en utilisant les conditions initiales pour déterminer les constantes d’intégration permet de remonter aux équations de Lagrange (Eq. 3.1). Le passage d’une méthode à l’autre est donc possible.