3.7. Exercices

3.7.1. Champ de vitesse d’une tornade 2D

Dans une tornade, la trajectoire de la particule fluide qui se trouve au point \(M_0\left(r_0,\theta_0\right)\) à l’instant t=0s à l’instant t=0s, a pour équations paramétriques en coordonnées polaires, de vecteurs de base \(\left({\vec{i}}_r,\ {\vec{i}}_\theta,{\vec{i}}_z\right)\) :

\(r=\sqrt{r_0^2-2at}\)

\(\theta=\theta_0-\frac{b}{2a}ln\left(\frac{r_0^2-2at}{r_0^2}\right)\)

  1. Donner l’expression du vecteur vitesse \(\vec{u}\), de l’accélération \(\vec{\Gamma}\) et celle du vecteur tourbillon \(\vec{\omega} = \frac {1}{2} \vec{\nabla} \land \vec{u}\).
  2. L’écoulement est-il stationnnaire, compressible?
  3. Quelle est l’équation générale des lignes de courant
  4. Décrire le mouvement d’une particule fluide initialement à \(M_0\left(r_0,\theta_0\right)\) . Est-ce réaliste ? Que manque -t-il dans cette description.
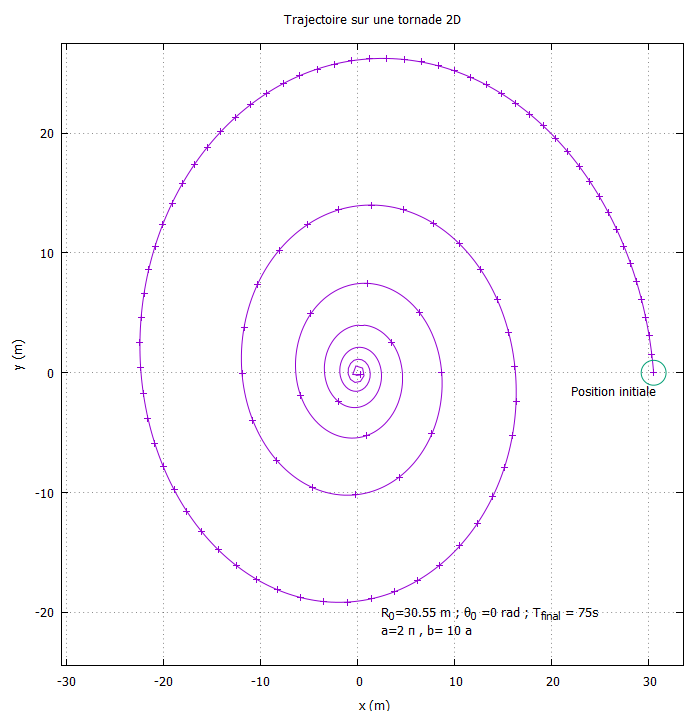
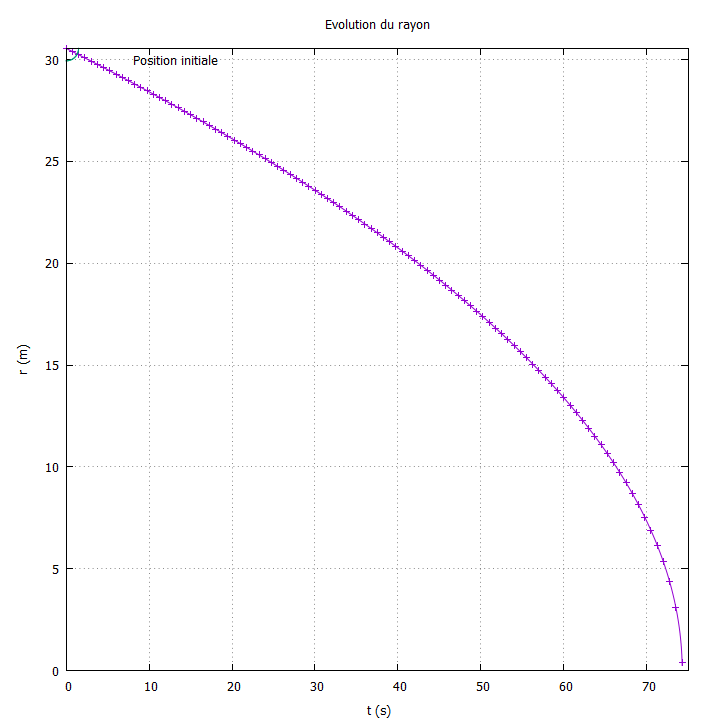
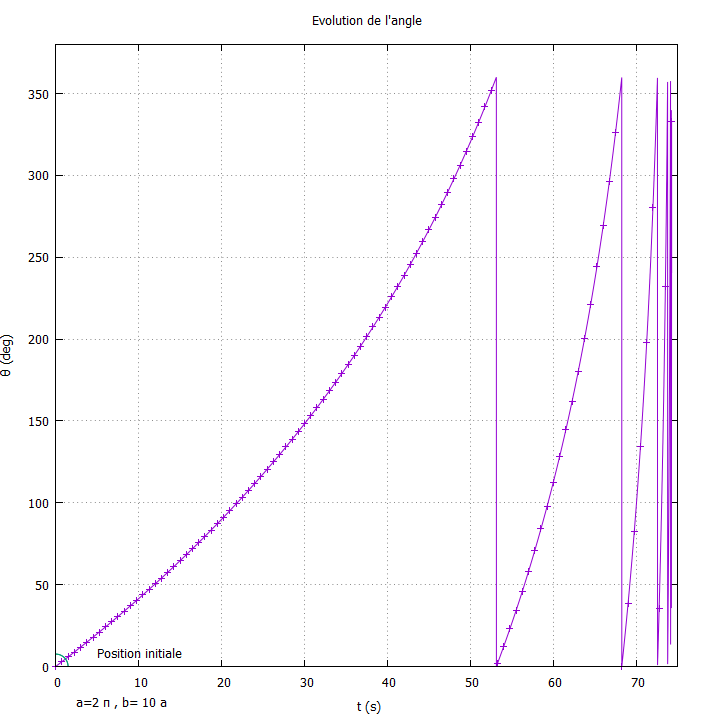
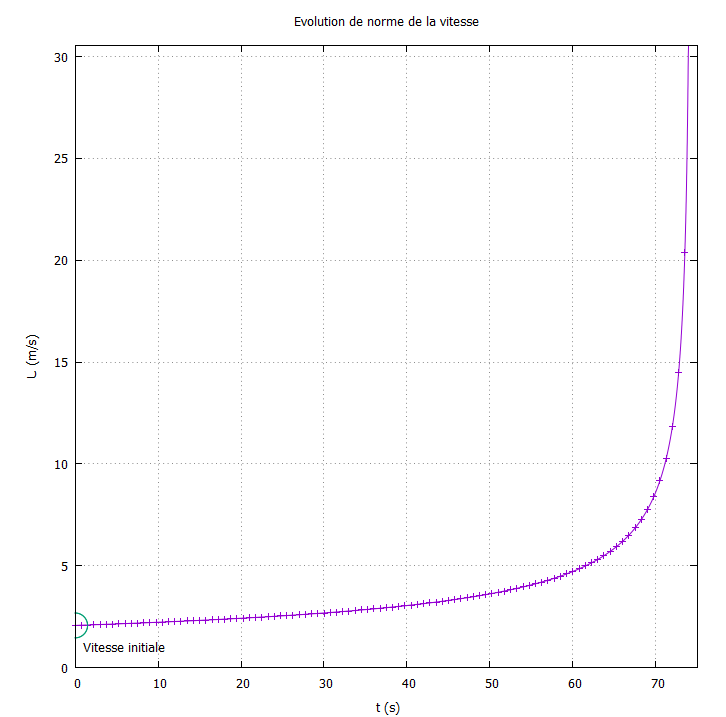
  5. Ecrire un programme qui permet de retrouver les résultats ci-dessous : Trajectoire, évolution du rayon et de l’angle en fonction du temps ainsi que la normae de la vitesse.

On prendra \(r_0 = 30.55m, \theta_0=0 rad\) \(t_{final}=75s\), \(a=2\pi\) et \(b=10a\)

_images/Trajectoire_tornade.png

Trajectoire d’une particule fluide initialement en \(M_0\left(r_0,\theta_0\right)\)

_images/RaysonVsTemps_tornade.png

Evolution du rayon en fonction du temps

_images/AngleVstemps_tornade.png

Evolution de l’angle en fonction du temps

_images/VitesseVsTemps_tornade.png

Evolution de la vitesse en fonction du temps

(Difficulté 4.5/5) Réponses:

  1. \(\vec{u}=-\frac{a}{r}{\vec{i}}_r+\frac{b}{r}{\vec{i}}_\theta\), \(\vec{\Gamma}=-\frac{a^2+b^2}{r^3}{\vec{i}}_r\) et \(\vec{\omega}=\frac{1}{2}\frac{b}{r^2}{\vec{i}}_z\)
  2. Stationnaire, compressible
  3. \(r=r_0e^{-\frac{a}{b}\left(\theta-\theta_0\right)}\)

3.7.2. Champ de vitesse 2D

On considère un écoulement dans le domaine \(x_1>0\) et \(x_2>0\) défini par le champ de vitesse suivant :

\(u_1=x_1\left(1+2t\right)\)

\(u_2=x_2\)

  1. Donner les principales caractéristiques de cet écoulement.
  2. Calculer les composantes et le module du vecteur accélération au point A(1,1) à t=0s.
  3. Trouver l’équation de la trajectoire qui passe par A à t=0s, sous la forme \(x_1=x_1(t)\) et \(x_2=x_2(t)\).
  4. Donner l’équation de la ligne de courant générale et celle qui passe par A à t=0s.

(Difficulté 4/5) Réponses:

  1. Ecoulement instationnaire, compressible, bidimensionnel.
  2. \(\vec{\Gamma}(A,0)={3\vec{i}}_1+{\vec{i}}_2\)
  3. \(\left\{\begin{matrix}x_1=e^{\left(t+t^2\right)}\\\ x_2=e^t\\\end{matrix}\right.\) et \(\vec{\Gamma}=\left\{\begin{matrix}\Gamma_1=2e^{\left(t+t^2\right)}+\left(1+2t\right)^2e^{\left(t+t^2\right)}=x_1(2+\left(1+2t\right)^2)\\\ \Gamma_2=e^t=x_2\\\end{matrix}\right.\)
  4. \(x_2=x_1\)