3.4. Taux de déformation¶
3.4.1. Tenseur taux de déformation¶
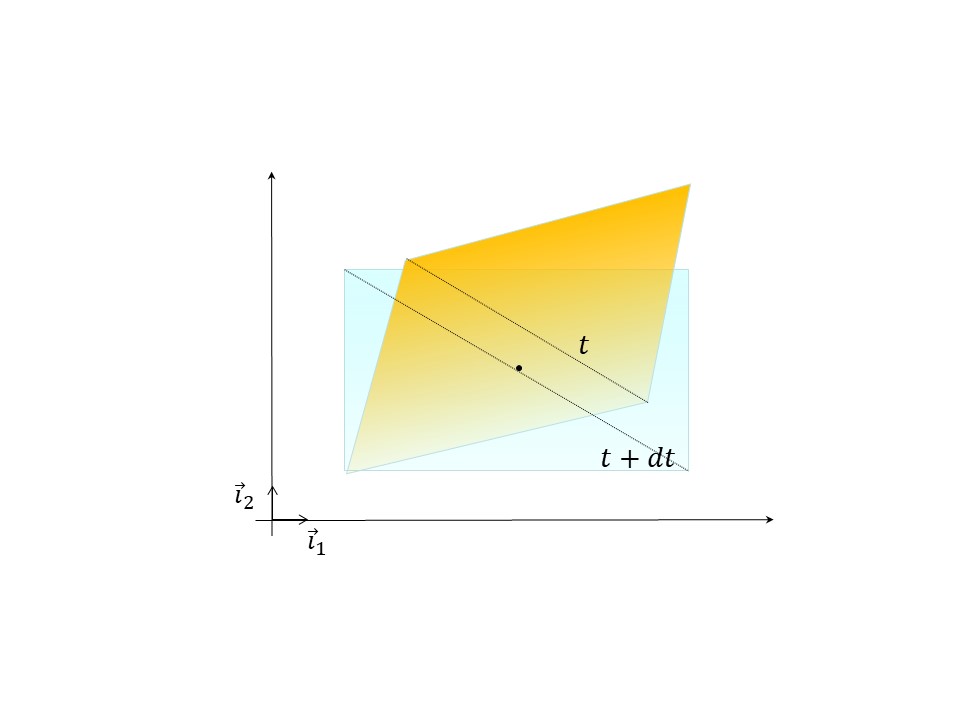
Pour calculer le taux de déformation d’un milieu continu en un point M de coordonnées \(X_M (\left(x_\alpha \right)_{\alpha=1,3})\), on considère le segment porté par le vecteur \(\vec{MN}\) avec \(X_N (\left(x_\alpha + \delta x_\alpha \right)_{\alpha=1,3})\).
Figure 3.5 : Variation au cours du temps d’unvecteur \(\vec{ds}\)
On définit le taux de variation \(\varepsilon\) par la variation de longueur du segment \(\vec{\delta s}=\vec{MN}\) par unité de temps et de longueur :
Avec :
Cette variation est calculée dans une direction matérielle \(\vec{b}\), vecteur unitaire tangent à la ligne matérielle \(\vec{MN}\), soit donc pour chaque coordonnée :
Dans la définition de \(\varepsilon\), pour éviter les calculs avec les racines carrées, on remarque que : \(\frac{d{\delta s}^2}{dt}\ = 2 \delta s \frac{d{\delta s}}{dt}\) soit \(\varepsilon=\lim\limits_{\delta s\rightarrow 0}{\left( \frac{1}{2} \frac{1}{{\delta s}^2} \frac{d{\delta s}^2}{dt} \right)}\)
On développe cette formule : \(\varepsilon=\lim\limits_{\delta s \to 0}{\left(\frac{1}{2} \frac{1}{{\delta s}^2}\frac{d \sum_{\alpha}{\delta x}_\alpha^2}{dt}\right) = \lim\limits_{\delta s \to 0}{\left(\sum_{\alpha}{\frac{\delta x_\alpha}{{\delta s}^2}\frac{d\delta x_\alpha}{dt}}\right)}}\)
Or, par définition du champ de vitesse : \(\frac{d\delta x_\alpha}{dt} = \frac{d(X_{N,\alpha}-X_{M,\alpha})}{dt}=V_{N,\alpha}-V_{M,\alpha}=\delta V_\alpha\)
Les coordonnées de la variation du champ de vitesse qui amène :
\(\varepsilon=\lim\limits_{\delta s \to 0}{\left(\sum_{\alpha}{\frac{\delta x_\alpha}{{\delta s}^2}\frac{d\delta x_\alpha}{dt}}\right)}=\lim\limits{\delta s \to 0}{\left(\sum_{\alpha}{\frac{\delta x_\alpha}{{\delta s}^2}\delta V_\alpha}\right)}\)
Si on écrit un DL du champ de vitesse autour de N on a :
\(V_{N,\alpha}=V_{M,\alpha}+\sum_{\beta}\frac{\partial V_{M,\alpha}}{\partial x_\beta}\delta x_\beta+\sum_{\beta}\frac{\partial^2V_{M,\alpha}}{\partial{x_\beta}^2}\delta^2x_\beta...\approx V_{M,\alpha}+\sum_{\beta}\frac{\partial V_{M,\alpha}}{\partial x_\beta}\delta x_\beta\).
Injectons ceci dans la dernière expression du taux de déformation :
\(...=\lim\limits_{\delta s \to 0}{\left(\sum_{\alpha,\beta}\frac{\partial V_\alpha}{\partial x_\beta}\frac{\delta x_\alpha}{\delta s}\frac{\delta x_\beta}{\delta s}\right)}\)
On reconnait les composantes du vecteur unitaire \(b\) :
On reconnait les composantes d’un tenseur d’ordre 2 qui définit en fait le tenseur de l’état des taux de déformation :
En coordonnées cartésiennes on à l’expression suivante :
\(\overline{\overline{\varepsilon}}=\sum_{\alpha,\ \beta}{{\vec{i}}_\alpha\frac{\partial}{\partial x_\alpha}u_\beta{\vec{i}}_\beta}=\sum_{\alpha,\ \beta}{{\vec{i}}_\alpha{\vec{i}}_\beta\frac{\partial u_\beta}{\partial x_\alpha}}\)
Dans le repère R, la représentation matricielle de ce tenseur s’écrit :
\(\overline{\overline{\varepsilon}}=\left[\begin{matrix}\frac{\partial u_1}{\partial x_1}&\frac{\partial u_1}{\partial x_2}&\frac{\partial u_1}{\partial x_3}\\\frac{\partial u_2}{\partial x_1}&\frac{\partial u_2}{\partial x_2}&\frac{\partial u_2}{\partial x_3}\\\frac{\partial u_3}{\partial x_1}&\frac{\partial u_3}{\partial x_2}&\frac{\partial u_3}{\partial x_3}\\\end{matrix}\right]\)
Les composantes de ce tenseur s’écrivent de façon générale : \(\varepsilon_{ij}=\frac{\partial u_j}{\partial x_i}\)
3.4.2. Analyse du tenseur des déformation¶
On vérifie facilement que le tenseur peut se décomposer en : \(\overline{\overline{\varepsilon}}=\overline{\overline{S}}+\overline{\overline{A}}\)
Une partie symétrique \(\overline{\overline{S}}\) telle que
Une partie anti-symétrique \(\overline{\overline{A}}\) telle que
Calculons \(S_{12}\) et \(A_{12}\) :
\(S_{12}=\frac{1}{2}\left(\frac{\partial u_2}{\partial x_1}+\frac{\partial u_1}{\partial x_2}\right) et\ A_{12}=\frac{1}{2}\left(\frac{\partial u_1}{\partial x_2}-\frac{\partial u_2}{\partial x_1}\right)\) Et on a bien \(\varepsilon_{12}={S_{12}+A}_{12}=\frac{\partial u_1}{\partial x_2}\)
3.4.3. Rotation en bloc¶
Si on définit le vecteur tourbillon de l’écoulement :
On a la relation:
qui représente la répartition des vitesses dans une rotation solide (ou en bloc) autour d’un axe passant par le centre de gravité de l’élément fluide.
Figure 3.6 : Rotation en bloc (sans cisaillement) avec le vecteur \(\vec{\Omega}\) d’un volume fluide dans le cas 2D
3.4.4. Dilatation-déformation angulaire¶
Tout tenseur symétrique peut se décomposer en un tenseur diagonal et un tenseur symétrique : \(\overline{\overline{S}}={\overline{\overline{S}}}_{diag}+{\overline{\overline{S}}}_{sym}\)
La partie diagonale du tenseur correspond aux composantes \(S_{\alpha\alpha}=\frac{\partial u_\alpha}{\partial x_\alpha}\)
Alors la trace de \(\overline{\overline{S}}\) et donc de \({\overline{\overline{S}}}_{diag}\) est égale à la divergence de la vitesse \(tr \left( \overline{\overline{S}} \right) =\vec{\nabla}.\vec{V}\)
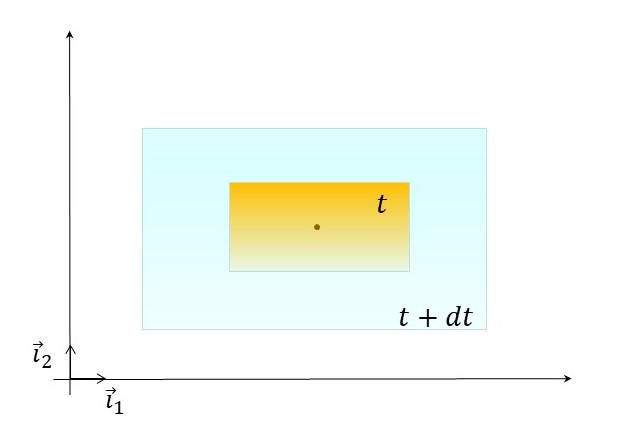
Figure 3.7 : Variation des longueurs d’un volume de fluide représentée par la partie diagonale du tenseur sphérique des taux de déformation- Cas 2D
On montre que \({\overline{\overline{S}}}_{diag}\) représente la variation de longueur dans chacune des directions \(x_\alpha\) : la vitesse de dilatation ou de contraction du volume fluide.
Figure 3.8 : Mouvement du au cisaillement (sans rotation) d’un volume de fluide - Cas 2D
On constate que si la variation est identique dans toutes les directions, \({\overline{\overline{S}}}_{diag}\) est un tenseur sphérique (physiquement, cela correspond à une sphère qui se dilate ou se contracte en gardant la même forme).
Important
Connaître le tenseur du taux des déformations sera très important quand on va lier ces déformations avec les forces qui les engendrent (lien contrainte-déformation).