3.5. Eléments de cinématique des fluides

3.5.1. Introduction

L’intérêt pratique de la cinématique réside dans la visualisation de l’écoulement. Supposons que l’on connaisse un écoulement, c’est-à-dire un champ de vitesse dans un domaine \(mathcal{D}\), quels sont les éléments mathématiques qui permettent une description géométrique de cet écoulement ? On connaît déjà les trajectoires, mais on aura besoin d’outils plus spécifiques selon que l’écoulement soit stationnaire ou pas.

3.5.2. Les trajectoires (pathlines)

Une trajectoire est une courbe formée par les positions successives d’une même particule donnée. L’équation de la trajectoire de la particule positionnée en \(\frac{{dx}_i}{dt}=u_i\left(X_{1,0},X_{2,0},X_{3,0},\ t \right)\)

On rappelle que \(x_i\) est la projection de la position du point M sur les axes du repère \(mathcal{R}\).

Une trajectoire est une courbe paramétrée par le temps qui est solution de :

(3.19)\[\boxed{\frac{{dx}_1}{u_1}=\frac{{dx}_2}{u_2}=\frac{{dx}_3}{u_3}=dt}\]

3.5.3. Les lignes de courant (streamlines)

On appelle ligne de courant, une ligne à un instant donné \(\tau\) telle que sa tangente coïncide avec le vecteur vitesse en ce point.

Figure 3.9 : Représentation d’une ligne de courant à un instante fixé \(\tau\)

La définition indique qu’un déplacement infinitésimal \(\vec{dl}\) sur la ligne de courant est parallèle à la vitesse, ce qui se traduit par la relation de colinéarité suivante \(\vec{dl}=\lambda\vec{u} \; ou \; \vec{dl}\times\vec{u}=\vec{0}\)

On écrit simplement que \(\vec{dl}=dx_1{\vec{i}}_1+dx_2{\vec{i}}_2+dx_3{\vec{i}}_3\) avec \(\lambda\) une constante réelle, on a donc à un instant \(\tau\) fixé: \(dx_i=\lambda_i\)

On résout en posant à \(\tau\) fixé :

(3.20)\[\boxed{ \frac{{dx}_1}{u_1}=\frac{{dx}_2}{u_2}=\frac{{dx}_3}{u_3}=\lambda }\]

On trouve une famille de courbes qui dépendent du temps \(\tau\).

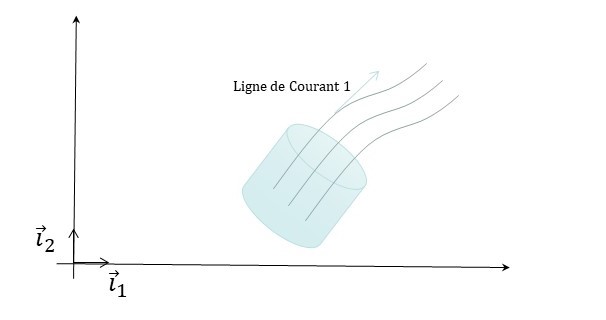
3.5.4. Les tubes de courant (streamtube)

Les tubes de courant sont formés par l’ensemble des lignes de courant qui s’appuient sur un contour fermé.

Figure 3.10 : Représentation d’un tube de courant

3.5.5. Lignes d’émission

Une ligne d’émission est le lieu géométrique à un instant donné \(\tau\), des particules fluides qui sont passées par un point donné et fixe de l’écoulement. En injectant de façon continue un colorant dans un écoulement à partir d’un point fixe on peut visualiser la ligne d’émission de ce point.

Indication

Dans le cas d’un écoulement permanent, qui ne dépend pas du temps, les trajectoires, les lignes de courant et les lignes d’émissions sont confondues et représentent la même chose.